 |
Моделирование
динамики популяций при помощи
электронной таблицы Excel. Уравнение
Лотка-Вольтерра как математическая
модель динамики системы "Хищник-жертва". |
| Моделирование
динамики популяции становится более
сложной задачей, если попытаться
учесть реальные взаимоотношения
между видами. Это
впервые сделал американский ученый А.Дж.
Лотка (A.J. Lotka) в 1925 г., а в 1926 г.
независимо от него и более подробно -
итальянский ученый В. Вольтерра (V.
Volterra). В модели, известной сейчас как Уравнение
Лотка-Вольтерра,
рассматривается взаимодействие двух
популяций - хищника и жертвы.
Численность популяции жертвы N1
будет изменяться во времени (завися
также от численности популяции
хищника N2) по такому уравнению: |
 |
где N1
- численность популяции жертвы, N2
- численность популяции
хищника, r1 -
скорость увеличения популяции жертвы
(т.е. рождаемость), p1 -
коэффициент хищничества для жертвы (вероятность
того, что при встрече с хищником
жертва будет съедена).
|
Таким образом,
увеличение численности жертвы в
единицу времени (выражение слева от
знака равенства и есть изменеие
численности dN1
за единицу времени dt)
происходит за счет рождения новых
особей (скорость размножения на
количество особей), а убыль - за счет
съедения хищниками (эта величина
пропорциональна численность жертвы,
т.к. чем больше, тем выше вероятность
встречи с хищником, численности
самого хищника и вероятности того,
что жертва при этой встрече погибнет p1).
Прирост популяции
хищника описывается таким
уравнением: |
 |
где N1
- численность популяции жертвы, N2
- численность популяции
хищника, d2 -
смертность хищника, p2 -
коэффициент хищничества (некая
величина, указывающая на "доход",
полученный хищником при поедании
жертвы).
|
| Рост популяции
хищника в единицу времени
пропорционален качеству питания (подразумевается,
что именно питанием ограничивается
рождаемость хищника, хотя явно это
нигде не указано), а убыль происходит
за счет естественной смертности. |
Попробуем при помощи электронной
таблицы Excel смоделировать динамику
численности двух популяций, выбрав
такие значения констант:
|
r1 =
0,1
|
p1 =
0,001 |
d2 = 0,05 |
p2 =
0,00005
|
| (выбранные
значения можно будет поменять, но это
уже следующий уровень сложности
работы). |
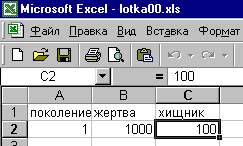
Создайте новую
книгу, в
которой на первом листе будут три
столбца - номер поколения,
численности жертвы и хищника (см. рис.
справа). Введите номер поколения (естественно,
1), а также начальную численности
жертв (1000 особей) и хищников (100 особей).
Чтобы не нумеровать поколения
вручную (а заодно потренироваться в
ведении формул в ячейки таблицы),
поступим так:
В ячейке А3 (под
единицей) кликнем левой кнопкой мыши
(активизируем ее) и введем
=A2+1
и нажмем [Enter]. (т.е.
в этой ячейке значение будет на
единицу больше, чем в предыдущей). |
 |
Теперь к
квадратику в правом нижнем углу
активной ячейки (А3) подведем курсор
мыши, и тогда он примет вид крестика.
Нажав левую кнопку мыши, растянем эту
ячейку вниз на столько поколений, на
сколько сочтете нужным.
Теперь введем в ячейку В3
формулу Уравнения Лотка-Вольтерра
для жертвы (вместо значений N1
и N2
пользуемся номерами ячеек, в которых
они находятся - В2 и С2
соответственно, а цифровые значения -
из таблицы выше):
=0,1*B2-0,001*B2*C2+B2 и нажмем [Enter]
(появление еще одного
слагаемого,
B2, связано с тем, что
формула показывает изменение
начальной численности, т.о. чтобы
получить количество особей второго
поколения, необходимо прибавить к
выражению численность предыдущего
поколения).
Теперь к квадратику в правом нижнем
углу активной ячейки (В3) подведем
курсор мыши (он опять примет вид крестика) и, нажав левую кнопку, растянем и эту
ячейку вниз на столько поколений, на
сколько сочтете нужным. При
этом численность жертвы начнет
экспоненциально возрастать, т.к. во
всех поколениях, кроме первого (по
мнению программы), хищников нет.
Теперь введем в ячейку С3
формулу для хищника (также вместо
значений N1
и N2
пользуемся номерами ячеек В2
и С2 и цифровыми
значениями из таблицы выше):
=0,00005*B2*C2 - 0,05*C2+C2 и нажмем [Enter]
Теперь снова растянем активную
ячейку (С3) на
выбранное число поколений.
Вы видите, что численности
установятся на исходных значениях 1000
и 100 особей соответственно, т.е.
популяции находятся в равновесии.
Разбалансируем систему. Для этого
изменим, например, численность жертвы
(кликнув на ячейке В2,
введем в строке формул новое
значение - например, 500 и нажмем [Enter]).
Программа сама пересчитает значения
во всех ячейках, и появятся колебания
численности обоих видов.
|
 |
Остается
представить результат в виде графика.
Для этого выделяем столбцы В
и С (достаточно
провести по их заголовкам с буквами
нажатой левой кнопкой мыши), и нажимаем
на иконку "Диаграмма"
на панели инструментов 
(или пункт меню Вставка
- Диаграмма). В открывшемся
диалоговом окне выбираем График и
соглашаемся с предлагаемым по умолчанию
графиком с маркерами. После
нескольких Далее> без возражений соглашаемся с Готово
и рассматриваем результат. Динамика
численности есть, но нагляднее было бы
представить значения численности обеих
популяций в согласованных величинах. |
|
Для этого кликните мышкой по любому
значению численности хищника, и в
открывшемся окне (Формат
ряда данных) выберите
закладку Ось,
а в ней в "Построить ряд"
выберите "По вспомогательной оси"
и нажмите ОК. Если было
просмотрено много поколений (100-200),
согласованные колебания численности
будут хорошо видны на графике. Если
поколений маловато, можно повторить
процедуры растягивания всех трех
столбцов еще на ряд поколений,
активизировав по очереди нижние ячейки
каждого и растягивая мышкой за правый
нижний угол.
|
 |
|
Все модели популяций в
